Примеры алгоритмов обработки деревьев и графов. Сравнение рекурсивных и итеративных алгоритмов, решающих некоторые классические задачи теории графов.
Содержание
В этой лекции мы рассмотрим некоторые классические алгоритмы, использующие графы и деревья, приведём и сравним рекурсивные и итеративные их варианты.
Используемая здесь терминология полностью совпадает с терминологией, введённой в предыдущей лекции.
Генерация дерева синтаксического анализа
Одно и то же арифметическое выражение может быть записано трёмя способами:
Инфиксный способ записи (знак операции находится между операндами):
((a / (b + c)) + (x * (y - z)))
Все арифметические операции, привычные нам со школьных лет, записываются именно таким образом.
Префиксный способ записи (знак операции находится перед операндами):
+( /(a, +(b, c)), *(x, -(y, z)))
Из знакомых всем нам функций префиксный способ записи используется, например, для sin(x), tg(x), f(x, y, z) и т. п.
Постфиксный способ записи (знак операции находится после операндов):
((a, (b, c)+ )/ ,(x, (y, z)- )* )+
Этот способ записи менее распространён, однако и с ним многим из нас приходилось сталкиваться уже в школе: примером будет n! (факториал).
Разумеется, вид дерева синтаксического анализа (ДСА)1 арифметического выражения не зависит от способа записи этого выражения (см. рис. 12.1), поскольку определяет его не форма записи, а порядок выполнения операций. Но процесс построения дерева, конечно же, зависит от способа записи выражения. Далее мы разберём все три варианта алгоритма построения ДСА.
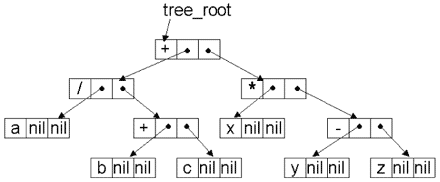
Рис. 12.1. Дерево синтаксического анализа и способ описания его элементов
tree = record
symbol : Char;
left : ukaz;
right : ukaz;
end;
Построение из инфиксной записи
Для простоты мы будем считать, что правильное арифметическое выражение подаётся в одной строке, без пробелов, а каждый операнд записан одной буквой. Приоритет операций определяется расставленными скобками: ими должна быть снабжена каждая операция.
Алгоритм Infix
Если не достигнут конец строки ввода, прочитать очередной символ.
Если этот символ — открывающая скобка, то:
- создать новую вершину дерева;
- вызвать алгоритм Infix для её левого поддерева;
- прочитать символ операции и занести его в текущую вершину;
- вызвать алгоритм Infix для правого поддерева;
- прочитать символ закрывающей скобки (и ничего с ним не делать).
Иначе:
- создать новую вершину дерева;
- занести в неё этот символ.
Реализация
Мы воспользуемся здесь описанием типа данных ukaz, приведённым на рис. 12.1:
var c : Char;
begin
Read(c);
if c = '(' then
begin
New(p);
infix(p^.left);
Read(p^.symbol); {'+', '-', '*', '/'}
infix(p^.right);
Read(c); {')'}
end
else
begin {'a' .. 'z', 'A' .. 'Z'}
New(p);
p^.symbol := c;
p^.right := nil;
p^.left := nil
end;
end;
begin
{...}
infix(root);
{...}
end.
Построение из префиксной записи
Для простоты предположим, что правильное арифметическое выражение подаётся в одной строке, без пробелов, а каждый операнд записан одной буквой. Кроме того, будем считать, что из записи удалены все скобки: это вполне допустимо, так как операция всегда предшествует своим операндам, следовательно, путаница в порядке выполнения невозможна.
Алгоритм Prefix
- Если не достигнут конец строки ввода, прочитать очередной символ.
- Создать новую вершину дерева, записать в неё этот символ.
- Если символ — операция, то:
- вызвать алгоритм Prefix для левого поддерева;
- вызвать алгоритм Prefix для правого поддерева.
Реализация
Вновь воспользуемся описанием типа данных ukaz, приведённым на рис. 12.1:
begin
New(p);
Read(p^.symbol);
if p^.symbol in ['+', '-', '*', '/'] then
begin
prefix(p^.left);
prefix(p^.right);
end
else
begin
p^.left := nil;
p^.right := nil;
end
end;
begin
{...}
prefix(root);
{...}
end.



 ::
::
 ::
::
 ::
::

